Set Theory
Set theory is the branch of mathematical logic that studies sets, which can be informally described as collections of objects. Founded by German mathematicians Richard Dedekind and Georg Cantor in the 1870s (Wikipedia).
Definitions
Set
A collection of objects, where order and repetition does not matter. Sets can hold any type of objects, not strictly 1 character numbers or letters.
Set Notation
Sets are usually surrounded by curly braces with commas separating elements and when assigned to a variable, the convention is to use a single capital letter (although there may be exceptions).
Element
The objects inside a set.
Element Notation
When you want to note a specific element from a set, you use the $\in$ symbol. When an element is not in a set, you use the $\notin$ symbol.
- Example: Written as $1 \in A$. Read/Spoken as “1 is an element of (set) A” OR “1 is a member of (set) A”.
- Example: Written as $34 \notin A$. Read/Spoken as “34 is not an element of (set) A” OR “34 is not a member of (set) A”.
Examples
$A = \{1, 2, 3, 4\}$. $B = \{a, b, c, d\}$. $C = \{cat, dog, cow, fox\}$.
Note: If you see “$\dots$” in a set that means that it should be clear what elements come next infinitely (i.e. this is the pattern for the set and it does not end).
Common Sets
These are special sets that are used across mathematics and computer science theory (algorithms).
Real numbers
- This set has any decimal number of any precision.
- Symbol: $\mathbb{R}$
- Examples: 1.0, 388.09384, 3.1415, -1005.6400009
Natural numbers
- This set has the counting numbers that you use everyday. Depending on context, they may start with 0 or 1, so be careful.
- Symbol: $\mathbb{N}$
- Example: $\{0, 1, 2, 3, 4, \dots\}$
Integers
- This set has any positive or negative whole number.
- Symbol: $\mathbb{Z}$
- Example: $\{\dots, -3, -2, -1, 0, 1, 2, 3, \dots\}$
Rational numbers
- This set has the result of dividing any two integers, but not 0 in the deminator.
- Symbol: $\mathbb{Q}$
- Examples: $\frac{3}{2}, \frac{2}{4}, \frac{-24}{97}$
Empty set
- This is the set that has no elements in it.
- Symbol: $\emptyset$ OR $\{\}$
Cardinality
Defintion
The size/length of the set.
Notation
Vertical bars around the name of the set.
Examples
- Let $A = \{1, 2, 3, 4\}$. The cardinality of set $A = |A| = 4$.
- Let $B = \{A, D, G, N, I, Y\}$. The cardinality of set $B = |B| = 6$.
Some sets are considered countable and some are considered uncountable. Simply, a set is countable if you can use the natural numbers to count the set in question. A set is uncountable if you cannout use the natural numbers to count it. There are also finite and infinite sets. A set is infinite is it has infinitely many elements and finite if it has a finite number of elements.
Subsets
Definition
One set is a subset of another if all of the elements of one set can be found in the other.
Notation
$A \subset B$ OR $A \subseteq B$. The “$\subset$” symbol is called “proper subset” and the “$\subseteq$” is called “subset”.
Note: There is a little line under the symbol in the second example. This subtle difference between the two symbols is similar to $<$ and $\le$.
Example of proper subset
Let $A = \{1, 2, 3, 4\}$ and let $B = \{1, 2, 3, 4, 5, 6, 7, 8\}$. In this case, $A \subset B$ because all of the elements in set $A$ can be found in set $B$, but $B$ has some elements that $A$ does not. That is how it is written, but when it is read/spoken, you say “(set) $A$ is a proper subset of (set) $B$”.
Example of subset
Let $A = \{1, 2, 3, 4\}$ and let $B = \{1, 2, 3, 4\}$. In this case, $A \subseteq B$ because all of the elements in set $A$ can be found in set $B$ and the two sets happen to be the same set. That is how it is written, but when it is read/spoken, you say “(set) $A$ is a subset of (set) $B$”.
Visually
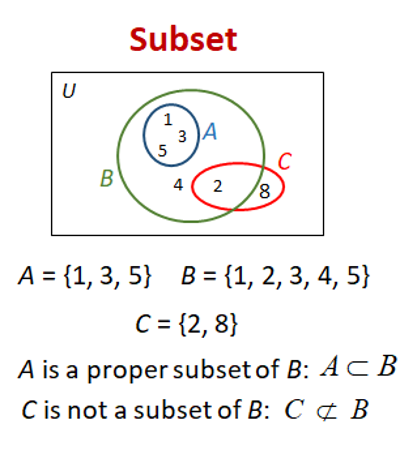
A visual example of subsets and proper subsets
Photo: OnlineMathLearning.com
(Click here to download the image if you want to save it for safe keeping.)
Note: The $U$ in the top left corner stands for the “universive of discourse”. You can think of this as the “domain” of the problem, where the universe has all possible values in a given problem.
Power Set
Definition
A power set of a set is the set of all possible subsets that can be made from the original set.
Notation
$\mathcal{P}(A)$
Example
Let $A = \{1, 2, 3\}$. $\mathcal{P}(A) = { {}, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3} }$.
Note: A quick check to make sure you didn’t miss a set when making the power set is to count the number of sets in your power set and see if it equals $2^{|A|}$. But this isn’t a complete/exhaustive check, so make sure you get every combination.
Note: The empty set is a subset of any set and therfore in every power set.
Common Set/Logic Operations
You can perform operations on sets. These operations are fairly common in discete math, algorithms, and logic/hardware. Some of the styles of notation may differ across these fields, but they all mean the same.
Union/OR
This operation is similar to an “addition” of the sets involved, like a combination. Combine the sets involved into one big set, but no duplicates. In set theory it is called “union” and in logic/hardware it is called “OR”.
Notation
Set theory: $A \cup B$. Logic/hardware: $A \lor B$.
Example
Let $A = \{1, 2, 3\}$ and let $B = \{3, 4, 5, 6\}$. The union of sets $A$ and $B$ is $\{1, 2, 3, 4, 5, 6\}$.
Intersection/AND
This operation is finding the commonalities bewtween the sets involved. In set theory it is called “intersection” and in logic/hardware it is called “AND”.
Notation
Set theory: $A \cap B$. Logic/hardware: $A \land B$.
Example
Let $A = \{1, 2, 3\}$ and let $B = \{3, 4, 5, 1\}$. The intersection of set $A$ and $B$ is $\{1, 3\}$.
Complement/NOT
In set theory, this operation is finding what is not in the set in question, but in logic/hardware, this operation is taking the opposite of a True/False value. This operation can be done in addition to other operations on one or more sets. It is also called a “negation”.
Notation
Set theory: $A^C$. Logic/hardware: $\bar{A}$ or $A'$, or $\sim A$.
Examples
Let the universe $U = \{1, 2, 3, 4, 5, 6\}$. Let $A = \{1, 2, 3\}$. Let $B = \{3, 4, 5, 1\}$.
- $A^C = \{4, 5, 6\}$
- $\overline{A \cup B} = \{6\}$
Note: In the last example, I used a very famous law/rule called DeMorgan’s Law, which will be left up to you to Google (very simple, but incredibly powerful trick). In short, DeMorgan’s Law lets you move a negation in and out of parantheses while maintaining the correctness of the answer.
Visually
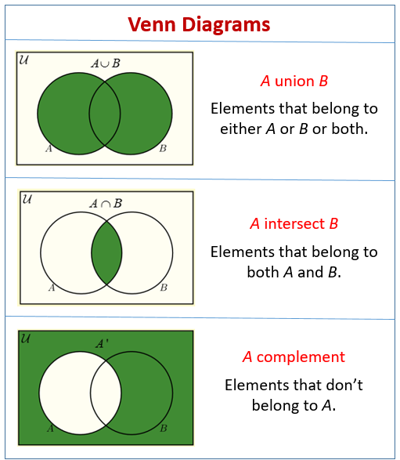
A visual example of subsets and proper subsets
Photo: OnlineMathLearning.com
(Click here to download the image if you want to save it for safe keeping.)
Note: Venn Diagrams are incredibly useful to visualize some of the set operations in more complicated problems that involve more than 2 simple, small sets. So if you are having trouble wrapping your head around a problem or operation when solving a problem, draw it out!